If he had a million dollars...
Thursday, July 24, 2008
...he probably would not have gotten caught snorting cocaine in New York...Or maybe it's because he does have a million dollars he was caught snorting snow...
I went to watch Batman this past Sunday, with Renee and Gabriel. Before the movie started, we were treated to the usual commercials we paid for (I always wonder how
they managed to get us to pay for advertisements). One of those commercials is about a couple of guys with a cooking show on some cooking channel. I've seen this ad a few times, but I never pay attention to it.
This time there was something peculiar about it. It was the buzz in the theater, which means that there is such a thing a bad publicity (
well, maybe). The singer from the Barenaked Ladies was in the commercial. That in itself is not weird at all; what was peculiar was that as soon as it came out he was no longer "the guy that sings in the Barenaked Ladies" but "the cokehead guy from the Barenaked Ladies"--this is a direct quote from a couple of people around my seat. In truth, it was the first thing that came to my mind, too: "hey, that's the guy that got caught doing coke."
I'm sure history will judge him better than we did, and he'll likely be known for being a singer and not for being a coke-junkie. In all fairness, he hasn't been tried for the crime, but he was arrested and charged for his partying ways.
Oh, and the movie...I don't want to spoil it for anyone, but Bruce Wayne is The Batman.
Robots can be useful
Tuesday, July 22, 2008
This is very impressive:
Full details.
Today's number theory naive algorithm: amicable or friendly numbers
Sunday, July 13, 2008
A pair of friendly numbers--the contemporary term is amicable numbers--are numbers such that "each is equal to the sum of the other's proper divisors (divisors other than the number itself)" (I got this definition from Paul Hoffman's book about Paul Erdos,
The Man Who Loved Only Numbers, p.45).
The first pair of friendly numbers is (220, 284), with their proper divisors [1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110] for 220, and [1, 2, 4, 71, 142] for 284.
Before I go onto my naive implementation to find pairs of friendly numbers, here is an easy problem:
prove that there are an infinite number of friendly pairs.
Where does this definition of
friendliness come from? From none other than
Pythagoras. He discovered the first pair (220, 284).
According to Hoffman, it took another 22 centuries for the second smallest pair (1184, 1210) to be found, by an Italian school boy in 1866.
I find it hard to believe that it took so long to get another pair, given that the algorithm to find them is obvious:
- Let A be an integer greater than 0; get the proper divisors of A.
- Add the divisors of A, and let the sum be equal to B.
- Get the divisors of B.
- Sum the divisors of B, and let the sum be equal to C.
- Finally, if B is equal to C, then we have a friendly pair.
I have to admit that doing this by hand can become a tedious and long process, but doable with a lot of time in your hands, a pen with a lot of ink, and a few sheets of paper (don't use a calculator, it takes the fun out of it).
I haven't studied the problem to come up with a short formula to generate these pairs of numbers (I haven't tainted my mind with web searches, so the algorithm and program are 100% my creation), but computers are very good at doing trivial math, so below is a very naive program to generate such pairs.
I say it's naive, because it's just a literal implementation of the algorithm I came up with above. The running time is horrible, because I check if every number between 1 and n/2 is a proper divisor of n. This thing is set to run for ever, and it's very fast to generate the first few pairs. As the program starts checking for larger numbers, it takes longer to find the proper divisors. It's also very dumb in the sense that it doesn't know that (66992, 66928) is the same as (66928, 66992), and it wastes cycles checking for both numbers even when we know that the proper divisors will be the same.
Note that generated pairs such as (28, 28) are not errors: the number in the pair has some special
properties, which I'm not qualified today to say what they are. Obviously, these generated pairs are not considered amicable numbers, even though they are part of the output in my program--I decide to leave them, as this is the first writing of the program.
[UPDATE: the number in this pair, is actually a
perfect number. It will take this program a long time to find them.]
A few interesting tidbits from running the program:
- The first 3 divisors are the same for even numbers (well, so far--and we know that running a program for a long time is not a mathematical proof).
- When I first looked at the definition, I thought only even numbers would be friendly pairs. I was obviously wrong, when I saw the pairs (12285, 14595), (69615, 87633).
- The largest pair I have so far is (308620, 389924). The app has only been running for about tow hours or so. Your mileage may vary.
The program (
some output):
import java.util.ArrayList;
public class FriendlyNumbers {
/**
* Calculate friendly numbers.
* A pair of friendly numbers are numbers such
* that each is equal to the sum of the other's
* proper divisors (divisors * other than the number itself).
*
* Example:
*
* (220, 284)
* Divisors for 220: [1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110]
* Divisors for 284: [1, 2, 4, 71, 142]
*
*
* @param args
*/
public static void main(String[] args) {
long testNumber1 = 1;
long testNumber2 = 0;
Divisors possibleFriendly1;
Divisors possibleFriendly2;
for (;;) {
possibleFriendly1 = getDivisors(testNumber1);
testNumber2 = possibleFriendly1.getSum();
possibleFriendly2 = getDivisors(possibleFriendly1.getSum());
if (testNumber1 == possibleFriendly2.getSum()
&& testNumber2 == possibleFriendly1.getSum()) {
System.out.println("------------");
System.out.println("(" + testNumber1 + ", "
+ testNumber2 + ")");
System.out.println("Proper divisors for "
+ testNumber1 + ": "
+ possibleFriendly1.getDivisors().toString());
System.out.println("Proper divisors for "
+ testNumber2 + ": "
+ possibleFriendly2.getDivisors().toString());
System.out.println("------------");
}
testNumber1++;
}
}
private static Divisors getDivisors(long testNumber) {
long sum = 0;
long possibleDivisor = 1;
ArrayList divisors = new ArrayList();
while (possibleDivisor <= (testNumber / 2)) {
if ((testNumber % possibleDivisor) == 0) {
divisors.add(possibleDivisor);
sum += possibleDivisor;
}
possibleDivisor++;
}
return new FriendlyNumbers.Divisors(sum, divisors);
}
static class Divisors {
private long sum;
private ArrayList divisors;
public Divisors(Long sum, ArrayList divisors) {
this.sum = sum;
this.divisors = divisors;
}
public long getSum() {
return sum;
}
public void setSum(long sum) {
this.sum = sum;
}
public ArrayList getDivisors() {
return divisors;
}
public void setDivisors(ArrayList divisors) {
this.divisors = divisors;
}
}
}
Naturally occurring nuclear fission
Friday, July 11, 2008
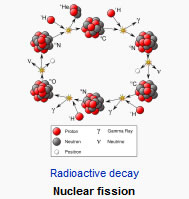
It was a big deal when Rutherford was able to split the atom in the early 19th century. The splitting of the atom meant that one element can be transformed into other elements. What's more, the amount of energy released is quite large (after all, E = mc
2).
This phenomena was a man made transformation. However, there is natural occurring fission. It's not very common, but it
happens:
A natural nuclear fission reactor is a uranium deposit where analysis of isotope ratios has shown that self-sustaining nuclear chain reactions have occurred. The existence of this phenomenon was discovered in 1972 by French physicist Francis Perrin. The conditions under which a natural nuclear reactor could exist were predicted in 1956 by P. Kuroda. The conditions found at Oklo were very similar to what were predicted.
At the only known location, three ore deposits at Oklo in Gabon, sixteen sites have been discovered so far at which self-sustaining nuclear fission reactions took place approximately 1.5 billion years ago, and ran for a few hundred thousand years, averaging 100 kW of power output during that time.
Mayonnaise: liquid or soft solid?
We know of 3 states of matter: gas, liquid, and solid (and plasma, I guess).
Now, under what classification does mayonnaise fall? It's not a liquid with high viscosity, or a soft solid. I know, I know: this is very important information. I guess I'll
google it.
For those curious enough, it's an
emulsion, or a mix of two (or more? I'm no chemist, so I don't know) liquids held together by something--in the case of mayonnaise, the something is egg.
Writing software for the Mars missions
There are probably few things that are cooler than writing software for the Mars missions. Well, writing any kind of software is cool enough, but seeing part of the thing you have created running in a different atmosphere must be thrilling.
The latest mission took about 1 million lines of C code, and thousands of men-hours.
Have a listen (or a read) to an interview with the main software engineer for the mission, Peter Gluck. The main intro goes as follows:
The Mars Phoenix Lander Mission is a short-term mission to Mars to search for signs of water and a potential habitable site for an eventual manned mission to the Red Planet. This mission is a collaboration between NASA and the University of Arizona Lunar and Planetary Laboratory.
Sending hundreds of pounds of equipment millions of miles through space to land and operate independently from direct control presents several interesting software development challenges. O'Reilly News recently discussed the project and its technology with NASA's Peter Gluck.
This is some fascinating stuff.
Computers are cool, but not this cool
Wednesday, July 09, 2008
What are top 5 things computers can do in movies:
compute the hell out of everything.
I only wish. Of course, computers can still do lots of crazy stuff, like let people write blogs and create useless stuff for people to create accounts in and have a gazillion friends.
When is
Web 3.0 coming? Enough social graphing stuff...
Today's conjecture: Golbach's conjecture
Monday, July 07, 2008
Every even integer greater than 2 can be written as the sum of two primes.I say, why not. Let's try it: 4 = 2 + 2 holds; 12 = 7 + 5 holds. Therefore, true.
Well, it's not proven yet, but why doubt your
intuition, right?
Now, a more interesting question: are there any
even primes? I think mathematicians are still looking for them. You see, they decided to check for odd primes first, and haven't gotten around checking for even primes. You know, with that whole deal of numbers being infinite and all. I'm hoping they finish with the odds sometime soon and just settle the
question of those even primes > 2.
Useless, but cool, JavaScript trick
Cut and paste one line of code to make any website editable.